The cleverest whisper: The RSA Algorithm.
Known by so many different names, The RSA algorithm, the Asymmetric Encryption or the Public-Private key cryptography is easily one of the pillars that hold the largest network known to us together: the internet. It’s clever. It’s efficient. And it feels seemingly “loophole free”. We’ve all played with Caesar Cipher; Caesar Cipher might just be the simplest example of cryptography (probably the oldest) that we can play with. What’s up with this fancy new stuff then? Well, our world has gotten a lot bigger and a lot more complex in the last century. We’ve had such great technological and scientific breakthroughs that if we stop evolving our cryptosystems, we might have a huge privacy problem, too. Of course, people don’t want their chats to be read or their pictures to be seen by hackers or just goofy governments for “national privacy”. That’s why we have encryption and that’s why we have RSA.

Ron Rivest, Adi Shamir and Leonard Adleman (their last name initials is where the letters in this cryptosystem come from) are one of the most prominent minds in cryptography and in computer science of all time. They developed the RSA algorithm in 1977 and, deservingly, got the Turing Awards for their remarkable breakthrough in 2002. Their idea was unconventional and unforeseen for their age and now is the base for our safe communications.
The Algorithm
It’s clever. The algorithm relies on two sets of keys. Public and Private. The public key, as the name suggests, is available to everyone (not really but anyone can access it and that won’t affect the security). The private key is private. Both the sender and receiver have their own private keys.
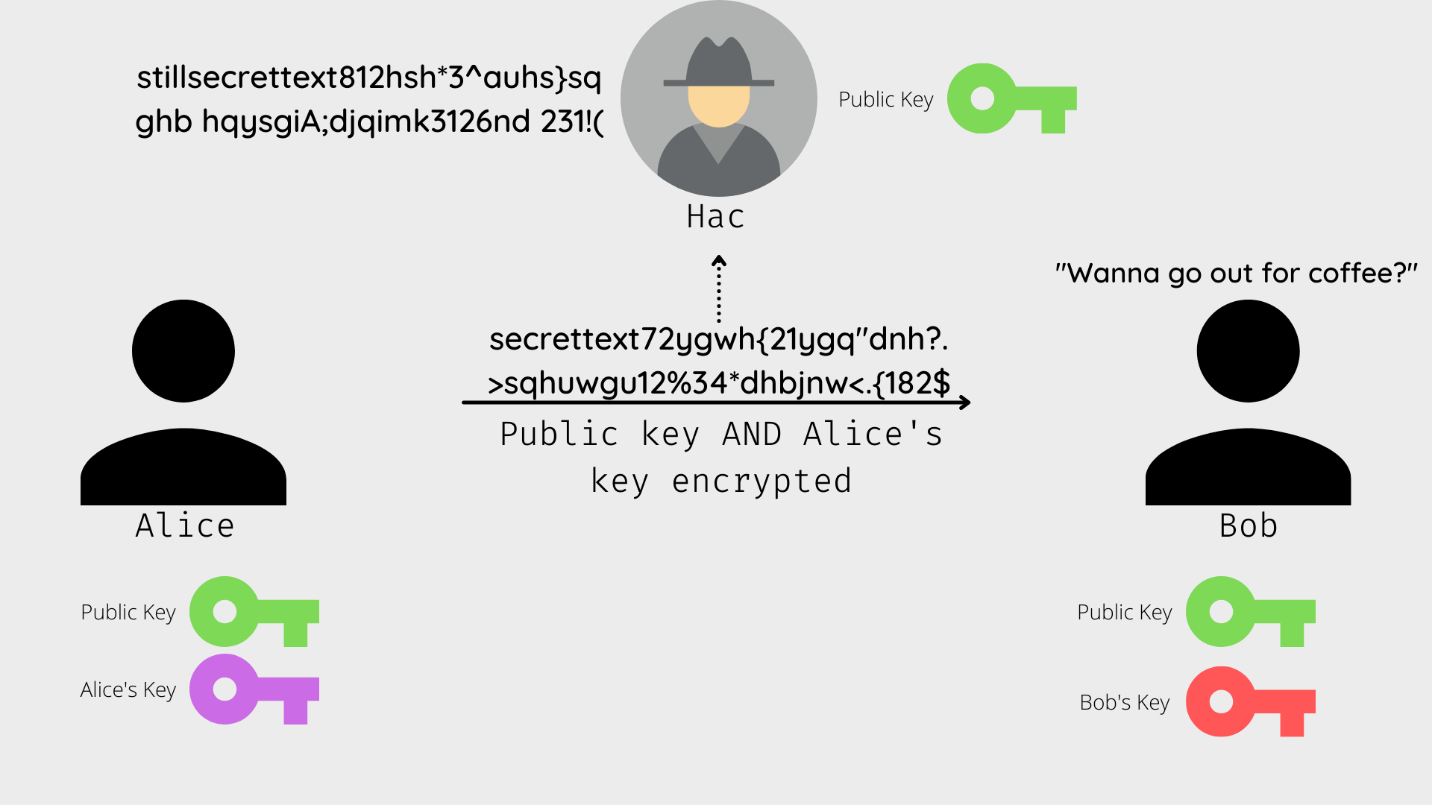
Let’s bring Alice and Bob to help us grasp this. Alice wants to contact Bob and ask him out for coffee, but she’s afraid Hac Erman would intercept their messages and come to the café too, which would just be horrendous for Alice and Bob (Hac is a HUGE pain in the butt). Alice and Bob decide to use the RSA encryption method to talk. Initially, Alice sends Bob a simple plain text message: “Hey, I wanna talk.”. This intrigues Hac, naturally, but Alice doesn’t care.

Bob reads the message and nods. He then creates two keys, the first key would encrypt Alices messages (thus, being the public key) and the second key would decrypt her messages (therefore, serving as Bob’s Private key). He then sends over the public key to Alice. Hac being the annoying person he is, gets his hand on the public key and thinks he’s making progress. Alice gets the key too.

She encrypts the message with the Public Key AND her own private key that she created. (The message was “Hey do you wanna go out for coffee?”). The message is double encrypted. Once, by the public key and then again by Alice’s key. When Alice sends the message, Hac will try to decrypt using the public key only to find out he needs Bob’s Private key, as well.
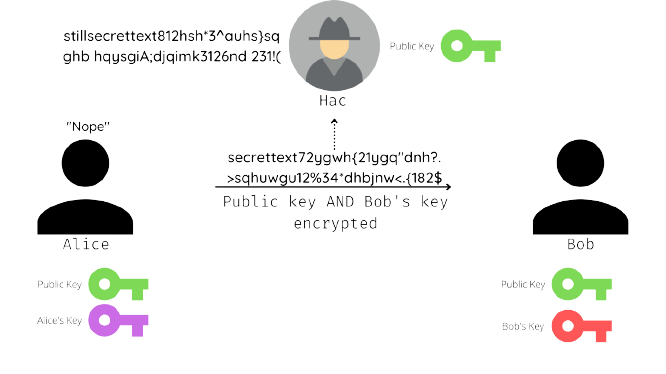
Bob receives the message, decrypts it first using a public key and then his own private key to read the message. He writes his own message: “Nope”. And encrypts it with both keys again. Alice finds the message, decrypts it with both the keys and frowns. The end.
If this analogy didn’t make sense to you and you’re a “math person”, perhaps this will satisfy you. If not, you might want to stop reading because things are about to get MATHSY *gasp*.
THE MATH.
Okay so, this example might be a simplification of the real process because obviously in real life, you’d require larger numbers (sometimes hundreds of digits) for the most impregnable cryptosystem. .
We know that we require two keys to decrypt a particular message: a public key and our own private key. Let me demonstrate the entire method first. Then, we’ll see HOW we got to the things we got to.
There we have it. Both our private keys and our public key. That, ladies and gentlemen, is the RSA cryptographic algorithm.